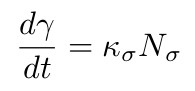Below are various pictures of geometric shapes which were mentioned in the course (some are just links to external sites).
Curve Shortening Flow
Minimal Surfaces
Curve Shortening Flow
We saw that curve shortening flow was given by a time dependant curve 
such that
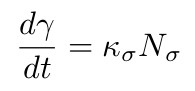We may calculate explicitly the evolution of a circle:
The Circle
The first results on the curve shortening flow demonstrated that convex curves shrink to points, as in this example.
Then, Gage and Hamilton observed that if we rescale (both in time and space) so that the area inside the curve remains constant then any convex curve converges to a circle as we may see here .
Finally Grayson's theorem shows that any curve becomes convex before it becomes singular, yeilding fantastic "uncoiling" phenomena as we may see here (apologies, I programmed this pretty quickly, there are some numerical errors which mean the final circle accellerates off to the bottom right, but you get the idea...).
Minimal Surfaces
We recall that a minimal surface is one with H=0, or equivalently it is a stationary point of the area (which we may hope is a minimiser of area, hence the name). We explicitly calculated curvatures of the catenoid and the helicoid .
I briefly mentioned
the Schwarz p-surface and also Costa's surface
However this is nothing. You should all definitely check out the
Minimal surfaces at the Virtual Mathematics Museum
these pictures are amazing. Check out the gyroid, the double Eneper surface, Riemann's surface...hours of clicking...Also I strongly recommend clicking on individual surfaces and scrolling on interactive pictures, looking at the 3d versions with 3d glasses etc.
